Навчальні матеріали
3. СУДЖЕННЯ ТА ЙОГО РОЛЬ В ЮРИСПРУДЕНЦІЇ
1. Судження як форма думки. Прості судження
Судженням називається така форма мислення, яка фіксує наявність або відсутність деякої ознаки у даного предмета думки. Судження може бути або істинним, або хибним.
У процесі пізнання об'єктивного світу людина розкриває зв'язки між предметами та їх ознаками, встановлює відношення між предметами. Ці зв'язки та відношення виражаються у мисленні у формі суджень, у вигляді зв'язку понять. Наприклад, висловлюючи судження "Петренко – курсант Національної академії внутрішніх справ", ми зв'язуємо поняття "Петренко" та "курсант Національної академії внутрішніх справ", відображаючи реальний зв'язок між конкретною особою та її ознакою.
Проблема суджень у логіці тісно пов'язана з теорією та практикою розслідування злочинів. Справа в тому, що судження (так само, як і поняття й умовиводи) дозволяє накопичувати інформацію. Крім того, норма права може розглядатись як судження. Без дотримання відповідних правил логіки неможливе моделювання правових норм.
Знання логіки суджень необхідне і для правильного тлумачення права. Слід також зазначити, що в процесі розкриття злочинних діянь, як і в логіці, судження використовуються для побудови умовиводів.
Зв'язки та відношення виражаються в судженні шляхом ствердження або заперечення. В судженні "Кожен злочинець повинен одержати заслужене покарання" зв'язок між злочинцем і необхідністю його покарання стверджується. В судженні "Деякі злочини не є умисними" зв'язок між певною частиною злочинних діянь та їх умисним характером заперечується.
Всяке судження може бути або істинним, або хибним, тобто відповідати дійсності або не відповідати їй. Якщо у судженні стверджується зв'язок, що існує в дійсності, або заперечується зв'язок, у дійсності відсутній, то таке судження буде істинним. Наприклад, "Крадіжка – злочин", "Тоталітарний режим не є демократичним" – істинні судження, вони правильно відображають реально існуючі або відсутні зв'язки. Якщо ж у судженні стверджується зв'язок, реально відсутній, або заперечується реально існуючий зв'язок, таке судження є хибним. Можна відповідно навести такі приклади: "Крадіжка – не злочин", "Тоталітарний режим є демократичним".
Слід, проте, мати на увазі, що не завжди істинність або хибність суджень буває явною або може бути легко встановлена. У низці випадків істинність суджень потребує відповідного обґрунтування. Не можна, наприклад, визнати істинним або хибним судження "Звинувачуваний зловживав службовим становищем", доки винність звинувачуваного у скоєнні даного злочину не доведена. Хоча об'єктивно, незалежно від нашого знання про даний факт це судження або істинне (якщо звинувачуваний справді зловживав службовим становищем) або хибне (у протилежному випадку), це ще треба встановити, що і є завданням карного судочинства.
Судження бувають простими і складними. Просте судження містить у своєму складі лише один суб'єкт, один предикат та одну зв'язку. Суб'єкт – поняття про предмет думки, який став предметом судження. Він позначається буквою "S". Предикат – поняття про ознаку або відношення, наявність чи відсутність яких приписується суб'єкту. Предикат позначається буквою "Р". Зв'язка виражається словами "є" або "не є" ("суть" або "не суть") і вказує, що саме – наявність чи відсутність вказаної у предикаті ознаки (відношення) стверджується судженням. Наприклад, у судженні "Вбивство є насильницьким позбавленням життя" "вбивство" – суб'єкт, "насильницьке позбавлення життя" – предикат, зв'язка виражається словом "є". У судженні "Дезертирство не є діянням, дозволеним Кримінальним кодексом" суб'єкт "дезертирство", предикат – "діяння, дозволене Кримінальним кодексом", зв'язка виражається словами "не є".
Розглянемо прості категоричні судження. Категоричними називаються судження, які виражають знання про належність тієї чи іншої ознаки предмету (або її неналежність останньому) незалежно від будь-яких умов.
Прості категоричні судження поділяються на види:
1) за якістю; 2) за кількістю; 3) за якістю і кількістю разом.
За якістю прості категоричні судження у свою чергу поділяються на дві категорії – стверджувальні та заперечні. Цей поділ залежить від характеру зв'язки. Якщо у судженні використано зв'язку "є" ("суть"), то воно стверджувальне, якщо ж "не є" ("не суть") – заперечне. Прикладами можуть слугувати наведені вище судження про вбивство та дезертирство. Перше з них є стверджувальним, друге – заперечним.
Логічний зміст простого судження можна виразити за допомогою формули. Наприклад, формула судження "Вбивство є насильницьким позбавленням життя" має такий вигляд: "S є Р". Логічний зміст судження "Дезертирство не є діянням, дозволеним Кримінальним кодексом" виражений у формулі S-(¬Р) "S не є Р" або "S є не-Р".
Заперечні судження відіграють у науці і практиці (в тому числі й юридичній) не менш важливу роль, ніж стверджувальні. Наприклад, судження "Жоден злочин не повинен залишитись нерозкритим" має дуже важливе значення для практичної діяльності. Можна було б навести і багато інших прикладів заперечних суджень.
У відповідності до їх кількісної характеристики прості категоричні судження можна поділити на одиничні, часткові та загальні.
Одиничним називається таке просте категоричне судження, у якому ознака співвідноситься з окремим предметом. Приклади: "Д. – працівник карного розшуку", "Ф. не порушував дисципліну" тощо.
Якщо у простому категоричному судженні ознака співвідноситься з частиною предметів деякої множини (класу), то воно називається частковим. Наприклад: "Деякі курсанти Національної академії внутрішніх справ – майстри спорту зі стрільби", "Інколи злочини бувають неумисними" тощо.
Загальним називається таке судження, в якому наявність або відсутність деякої ознаки стверджується відносно кожного предмета множини, вираженої у суб'єкті. Приклади: "Всі слухачі першого курсу повинні складати залік з логіки", "Жодне злочинне діяння не повинне залишитися безкарним".
Крім того, ми можемо визначати одночасно обидві характеристики простого категоричного судження – і якісну, і кількісну. Тут має місце поділ за якістю і кількістю разом. Він дає чотири категорії суджень: загальностверджувальні, загальнозаперечні, частковостверджувальні і частковозаперечні.
Загальностверджувальне – таке просте категоричне судження, в якому стверджується наявність певної ознаки у всіх предметів даної множини (класу). За якістю воно стверджувальне, а за кількістю – загальне. Приклад такого судження ми вже розглядали ("Всі слухачі першого курсу повинні складати залік з логіки"). Інші приклади: "Всі діяння, передбачені Кримінальнним кодексом, є злочинами", "Всі міркування необхідно будувати з додержанням вимог логіки" тощо.
Логічний зміст загальностверджувального судження можна виразити за допомогою формули. Крім суб'єкта, предиката і зв'язки вона містить ще один елемент – квантор. Це логічний оператор, який несе кількісну характеристику логічного виразу. Розрізняють квантор загальності та квантор існування. Квантор загальності у природній мові виражається найчастіше словами "всі" і "жоден" ("жодна", "жодне"), квантор існування – словом "деякі".
Квантор загальності позначається символом "∀" або буквою "а". Формула загальностверджувального судження має такий вигляд: ""∀S-Р" або "SаР" і читається так: "всі S є Р". Його можна також скорочено позначити через букву А.
Загальнозаперечним простим категоричним судженням називається таке судження, в якому стверджується відсутність ознаки у множини предметів. За кількістю воно загальне, за якістю – заперечне. Ми вже мали приклад такого судження: "Жодне злочинне діяння не повинне залишитись безкарним". Можна навести й інші: "Жоден суддя, зацікавлений у результатах справи, не може брати участь у розгляді цієї справи", "Слухачі не мають права порушувати дисципліну" тощо. Квантор загальності в даному випадку може виражатись за допомогою букви "е" і формула загальнозаперечного судження має два варіанти: "∀ S-(¬Р)" або SеР.
Вони читаються так: "жоден S не є Р".
Скорочено загальнозаперечне судження позначається через букву Е.
Частковостверджувальним називається таке просте категоричне судження, в якому стверджується наявність ознаки у певної частини елементів множини. За кількістю воно часткове, за якістю – стверджувальне. Приклади такого судження: "Деякі курсанти Національної академії внутрішніх справ – майстри спорту із стрільби", а також "Певній частині слухачів логіка дається важко", "Деякі злочинці є рецидивістами" тощо.
Для формалізації даного судження використовується квантор існування, що виражається за допомогою символу "∃". У випадку частковостверджувального судження його можна позначити через букву "і".
Формулу можна записати двома способами:
"∃S-Р" або SіР.
Читається вона так: "деякі S є Р" або "існують S, що є Р" (другий варіант і пояснює походження назви квантора існування). Скорочено частковостверджувальне судження позначається через букву І.
У частковозаперечному простому категоричному судженні стверджується відсутність ознаки у частини елементів множини. За кількістю воно часткове, за якістю – заперечне. Для прикладу можна розглянути судження "Інколи злочини не є умисними", а також "Деякі судження не є стверджувальними", "Не кожен слухач має спортивний розряд" тощо.
У формулі частковозаперечного судження квантор існування може бути позначений через букву "о"; тут можливі такі варіанти: "∃S-(¬Р)" або "SоР".
Обидва варіанти читаються однаково: "деякі S не є Р" (або існують S, що не є Р)". Скорочено частковозаперечне судження позначається через О.
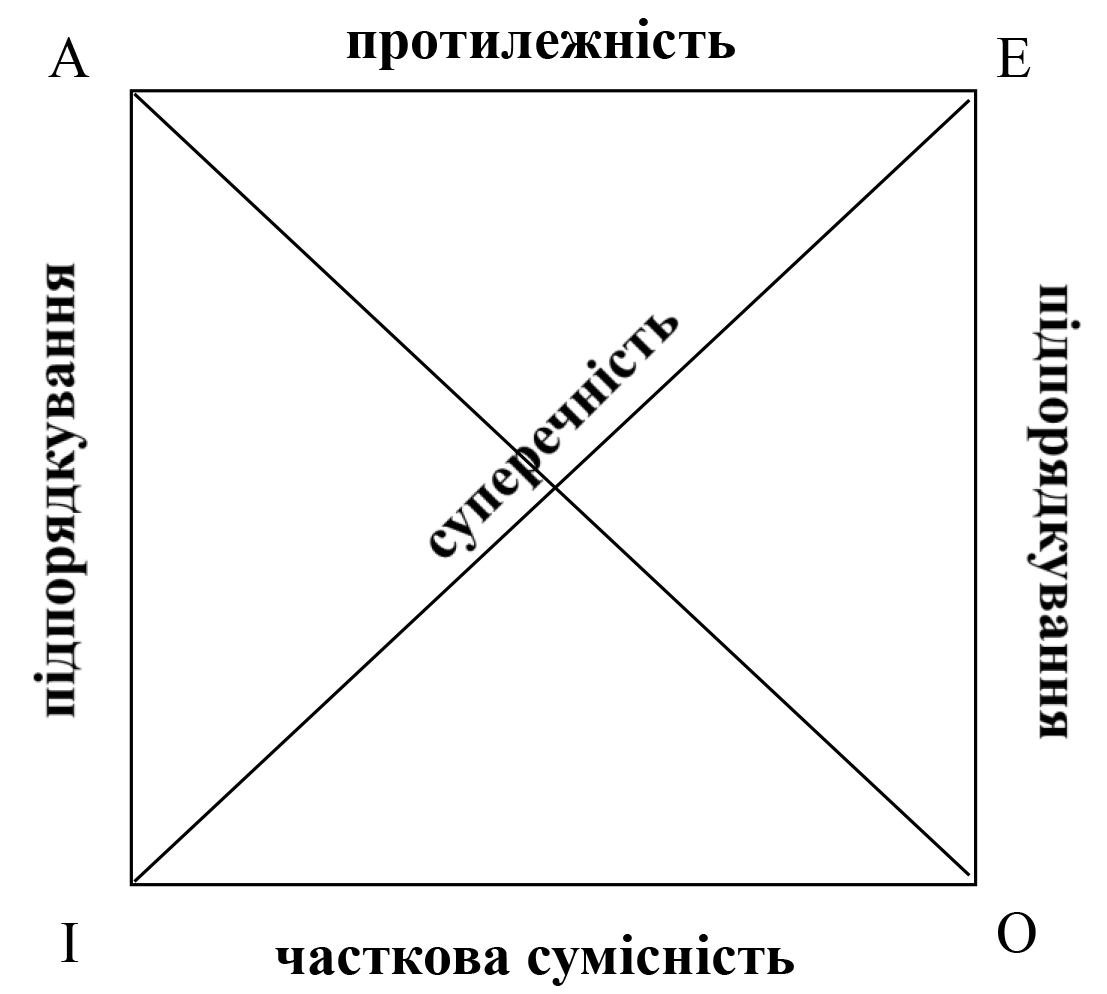
Якщо загальностверджувальне, загальнозаперечне, частковостверджувальне та частковозаперечне судження мають той самий суб'єкт і той самий предикат, то між ними мають місце дуже цікаві зв'язки. Вони виражаються за допомогою схеми, котра отримала назву "логічного квадрату". Ось вона:
Для прикладу надамо буквам таких значень:
А – "Всі курсанти даної групи є спортсменами";
Е – "Жоден курсант даної групи не є спортсменом";
І – "Деякі курсанти даної групи є спортсменами";
О – "Деякі курсанти даної групи не є спортсменами".
Слова "протилежність", "суперечність", "підпорядкування" та "часткова сумісність" вказують логічні відношення між відповідними простими категоричними судженнями. Нам треба з'ясувати їх сенс. Звернімося до реальних ситуацій, пов'язаних зі змістом даних суджень. Видимо, існують такі три варіанти. По-перше, існують такі групи курсантів, в яких кожен є спортсменом. По-друге, треба згадати групи, в яких спортсменів нема. І, нарешті, можна знайти й такі групи, в яких частина слухачів займаються спортом, а частина – ні.
Оцінимо тепер характер відповідності між нашими судженнями – загальностверджувальним, загальнозаперечним, частковостверджувальним та частковозаперечним, з одного боку, та цими реально можливими ситуаціями. Їх зручно виразити за допомогою такої таблиці:
|
А |
Е |
О |
І |
|
|
1. Кожен курсант – спортсмен |
||||
|
2. Спортсменів у групі нема |
||||
|
3. Частина курсантів спортсмени, частина – ні |
Сформулюємо запитання: "Яким є А – істинним чи хибним по відношенню до кожної з даних ситуацій?". Будемо позначати істинність через І, хибність – через Х. Відповіддю буде такий стовпчик у нашій таблиці:
|
А |
Е |
О |
І |
|
|
1. Кожен курсант – спортсмен |
І |
|||
|
2. Спортсменів у групі нема |
Х |
|||
|
3. Частина курсантів спортсмени, частина – ні |
Х |
Поставимо те саме запитання відносно загальнозаперечного судження (Е). Одержимо другий стовпчик:
|
А |
Е |
О |
І |
|
|
1. Кожен курсант – спортсмен |
І |
Х |
||
|
2. Спортсменів у групі нема |
Х |
І |
||
|
3. Частина курсантів спортсмени, частина – ні |
Х |
Х |
Третій стовпчик одержимо, оцінивши відношення до даних ситуацій судження типу І (частковостверджувального). Але тут необхідне певне уточнення. Якщо в групі кожен курсант – спортсмен, то частковостверджувальне судження, строго кажучи, треба визнати істинним. Його можна розуміти так, що принаймні деякі курсанти групи – спортсмени. Дане судження містить не всю інформацію про групу, якщо насправді кожен із слухачів – спортсмен, але та інформація, яку воно містить, істинна. Варто відзначити, що подібна ситуація має місце й у юриспруденції. Скажімо, у суді виступає свідок і каже, що він колись вчився разом із підсудним і що деякі слухачі їх групи були спортсменами, а суду відомо, що вся група складалась із спортсменів. Чи є підстави для того, щоб звинуватити свідка у хибному свідченні? Таких підстав нема. Його інформація не зовсім повна, вона стосується лише частини слухачів, але вона відповідає дійсності. Цей момент враховується й у логіці. Тому судження "Деякі курсанти даної групи спортсмени" по відношенню до першої ситуації треба визнати істинним і таблиця одержує третій стовпчик:
|
А |
Е |
О |
І |
|
|
1. Кожен курсант – спортсмен |
І |
Х |
І |
|
|
2. Спортсменів у групі нема |
Х |
І |
Х |
|
|
3. Частина курсантів спортсмени, частина – ні |
Х |
Х |
І |
Останній стовпчик (він характеризує відношення до трьох вказаних ситуацій частковозаперечного судження) визначається аналогічно. Повністю таблиця виглядає так:
|
А |
Е |
О |
І |
|
|
1. Кожен курсант – спортсмен |
І |
Х |
І |
Х |
|
2. Спортсменів у групі нема |
Х |
І |
Х |
І |
|
3. Частина курсантів спортсмени, частина – ні |
Х |
Х |
І |
І |
Яке відношення має дана таблиця до логічного квадрату? Вона містить точні відповіді на запитання, що таке суперечність, протилежність, підпорядкування і часткова сумісність. Наприклад, щоб виявити суть відношення суперечності, треба звернутись до стовпчиків Е та І (або А і О), між якими має місце дане відношення. Відповідь має такий вигляд: якщо два судження знаходяться у відношенні суперечності, то можливі два варіанти: перше хибне, друге істинне або перше істинне, а друге – хибне. Більше можливостей нема.
Щоб виявити сенс відношення протилежності, треба взяти стовпчики, які відповідають судженням А та Е, що знаходяться у цьому відношенні. Одержимо таку інформацію: перше судження хибне, друге – істинне, або перше хибне і друге істинне, або обидва судження хибні. Тут отримали три варіанти.
Якщо загальне судження підпорядковує часткове, то маємо три можливості: обидва судження одночасно істинні, обидва судження хибні або загальне хибне, хоча часткове – істинне. Таку інформацію дають стовпчики А та І (або Е та О).
Нарешті, суть відношення часткової сумісності розкривається стовпчиками І та О. Вона полягає в тому, що можливі також три варіанти: перше судження істинне при другому хибному, або перше хибне при другому істинному, або обидва істинні.
Слід нагадати, що розглянуті нами відношення існують між загальностверджувальним, загальнозаперечним, частковостверджувальним і частковозаперечним судженнями тоді і лише тоді, коли вони мають тільки один спільний суб'єкт і тільки один спільний предикат. Тобто можна сказати, що вони повинні відрізнятись одне від одного тільки за якістю і кількістю. Якщо між ними є відмінності щодо суб'єкта або предиката, вказаних у логічному квадраті відношень може і не бути.
Перейдемо до другого питання плану.
2. Складні судження, їх види та семантичні таблиці
Важливу роль в юридичній теорії та практиці відіграють складні судження. Складними називаються судження (висловлювання), утворені з двох або більше простих (елементарних) суджень. Складні судження є результатом відповідних операцій із простими судженнями, а саме кон'юнкції, диз'юнкції (слабкої чи сильної, нестрогої чи строгої), імплікації та еквіваленції. Ці операції здійснюються за допомогою однойменних операторів, які мають свої символічні позначення:
- кон'юнкція : ∧;
- диз'юнкція слабка (нестрога): ∨;
- диз'юнкція сильна (строга): ∨;
- імплікація : →;
- еквіваленція : ↔.
Їх можна розглядати і як логічні сполучники (зв'язки). Крім них, при роботі з простими судженнями використовується оператор заперечення. Він позначається символом ¬ або рискою над відповідною змінною.
Прості судження позначаються через букви латинського алфавіту (А, В, С тощо). Вони виступають як змінні.
Розглянемо операції з простими судженнями докладніше.
Якщо взяти прості судження "П.– відмінник навчання" та "П. – майстер спорту із самбо", то за допомогою кон'юнкції можна одержати складне судження "П. - відмінник навчання і майстер спорту із самбо". Воно називається також кон'юнкцією або сполучним судженням. Його формула має такий вигляд: "А ∧ В". Оператор кон'юнкції виражається в українській мові граматичним сполучником "і" ("та"). Формула читається так: "А кон'юнкція В", "А і В", "А та В".
Взагалі кажучи, між логічним оператором (сполучником) кон'юнкції та граматичним сполучником "і" ("та") існує принципова відмінність. Найбільш повна і точна відповідь на запитання про суть логічного оператора (сполучника) кон'юнкції, його функціональний сенс міститься у так званій семантичній таблиці (або таблиці істинності).
Нехай у нас є деякі прості судження А та В. Припустімо також, що вони семантично незалежні одне від одного, тобто істинність або хибність А не тягне за собою істинності або хибності В, і навпаки. Тоді істинність сполучного судження "А ∧ В" буде функцією істинності суджень А і В. Зрозуміло, що для двох семантично незалежних суджень можливі лише такі чотири комбінації:
1) А і В обидва істинні;
2) А істинне, В хибне;
3) А хибне, В істинне;
4) А і В обидва хибні.
Щодо кон'юнкції "А ∧ В" має місце така залежність: вона істинна, тільки якщо А і В істинні, і хибна у решті випадків. Істинність судження у логіці прийнято позначати через одиницю, хибність – через нуль, і відповідна таблиця виглядає так:
|
А |
В |
А ∧ В |
|
1 |
1 |
1 |
|
1 |
0 |
0 |
|
0 |
1 |
0 |
|
0 |
0 |
0 |
Звідси стає зрозумілою основна відмінність між логічним оператором (сполучником) кон'юнкції, який у мові передається словами "і", "й", "та", і граматичним сполучником "і" ("й", "та"). Останній звичайно використовується для сполучення суджень, які мають щось спільне за змістом. А за допомогою кон'юнкції можна сполучати одне з одним будь-які судження. Єдина вимога для того, щоб кон'юнктивне судження було істинним, полягає у істинності всіх простих суджень, які входять до його складу.
Розглянемо тепер оператор диз'юнкції. Існує два його різновиди: слабка (нестрога) диз'юнкція і сильна (строга). Почнемо з першого.
Можна взяти такі прості судження: "Відмінник повинен бути здібним" і "Відмінник повинен багато працювати". Їх можна об'єднати у складне за допомогою слабкої диз'юнкції. Результат буде виглядати так: "Відмінник повинен бути здібним або багато працювати". Це судження називається нестрого-розділовим або слабкою диз'юнкцією. Його структура відображається такою формулою: "А ∨ В". У мові оператор (сполучник) слабкої диз'юнкції, як правило, передається граматичними сполучниками "чи", "або". Читається формула так: "А слабка диз'юнкція В", "А чи В", "А або В".
Судження слабкої диз'юнкції, подібно до кон'юнктивного, є функцією істинності суджень А і В. Але, звичайно, це інша функція істинності: хоча істинність або хибність судження "А ∨ В" повністю визначається істинністю або хибністю простих суджень, що входять до його складу, визначається вона, проте, інакше. Слабка диз'юнкція характеризується такою залежністю: вона хибна лише за умови хибності всіх простих суджень, які входять до його складу. Ось його семантична таблиця, яка дає точну характеристику його функціонального значення:
|
А |
В |
А ∨ В |
|
1 |
1 |
1 |
|
1 |
0 |
1 |
|
0 |
1 |
1 |
|
0 |
0 |
0 |
Тут також варто підкреслити відмінність між логічним оператором (сполучником) слабкої диз'юнкції та граматичним сполучником "чи" ("або"). Якщо ми маємо справу з логічним оператором, то зв'язок між складовими – простими судженнями не є обов'язковим.
Для того, щоб продемонструвати операцію сильної (строгої) диз'юнкції, зручніше взяти інші прості судження, наприклад: "Підсудний винен" і "Підсудний не винен". В результаті названої операції отримаємо судження "Підсудний або винен, або не винен". Воно називається строго-розділовим або сильною (строгою) диз'юнкцією. Формула даного судження: "А ∨ В". В усній мові й на письмі цей оператор найчастіше виражається за допомогою граматичного сполучника "або..., або...". Формула читається так: "А сильна диз'юнкція В", "А строга диз'юнкція В", "або А, або В".
"А ∨ В" як функція істинності А і В характеризується такою залежністю: воно істинне у двох випадках: якщо А істинне, а В хибне, або якщо А хибне і В істинне. У решті випадків дане складне судження хибне. Функціональне значення цього оператора виражається такою таблицею:
|
А |
В |
А ∨ В |
|
1 |
1 |
0 |
|
1 |
0 |
1 |
|
0 |
1 |
1 |
|
0 |
0 |
0 |
Тут смисловий зв'язок між судженнями А і В не є необхідним. Для істинності судження сильної диз'юнкції досить, щоб обидва судження – А і В – не були одночасно істинними або одночасно хибними.
Наступний оператор, який ми розглянемо – іплікація. Нехай у нас є прості судження: "Особа вчинила грабіж" і "Особа є злочинцем". Їх можна об'єднати у таке складне судження: "Якщо особа вчинила грабіж, то вона є злочинцем". Це судження називається умовним або імплікацією. Його формула має такий вигляд: "А → В". Читається вона так: "А імплікація В", "якщо А, то В", "з А випливавє В" тощо.
Варто зауважити, що імплікація відрізняється від усіх інших розглянутих логічних операторів тим, що вона є асиметричною, в той час як решта операторів – симетричні. Інакше кажучи, у кон'юнкції і диз'юнкції (як слабкій, так і сильній) можна поміняти місцями складові – прості судження, і це не матиме жодних наслідків. Тобто якщо до формул "А ∧ В", "А ∨ В" та "А ∨ В" А і В входитимуть в іншому порядку (отримаємо тоді "В ∧ А", "В ∨ А" та "В ∨ А"), то це не призведе до зміни їх семантичних (істиннісних) характеристик – істинне судження не стане хибним, а хибне – істинним. У випадку імплікації ситуація інша. Формула "А → В" містить твердження, що саме з А випливає В, а не навпаки. Перше судження (А) називається підставою (засновком, антецедентом), друге (В) – наслідком (висновком, консеквентом). Порядок їх входження до формули не можна змінювати – якщо "А → В" істинне, то "В → А" може бути хибним, якщо перше було хибним, то друге може виявитись істинним.
Імплікація – нова функція істинності простих суджень, які входять до її складу. Тут має місце така залежність:" А → В" вважається хибним лише за однієї умови – якщо А істинне, а В хибне. Це відповідає змістовному уявленню про те, що умовне судження не може бути істинним, якщо при істинній підставі наслідок виявляється хибним. У решті випадків імплікативне судження розглядається як істинне. Семантична таблиця, що характеризує функціональне значення імплікації, виглядає так:
|
А |
В |
А → В |
|
1 |
1 |
1 |
|
1 |
0 |
0 |
|
0 |
1 |
1 |
|
0 |
0 |
1 |
Ми бачимо, що логічний оператор (сполучник) імплікації помітно відрізняється за своїм сенсом від граматичного сполучника "якщо..., то..." ("коли..., тоді..."). У природній мові "якщо..., то..." виражає причинну залежність або який-небудь інший змістовний зв'язок слідування між А і В. Імплікація ж (так само, як й інші логічні оператори) може об'єднувати у складне й такі прості судження, які не по"вязані одне з одним за змістом. Наведена таблиця є точним означенням імплікації як логічного оператора.
Останній оператор нашої групи – еквіваленція. (тотожність). Його можна застосувати, щоб отримати складне судження, наприклад, з таких простих: "Постріл зроблено з близької відстані" і "На тілі жертви залишилась штанцмарка". (Кажуть, що на тілі є штанцмарка, якщо внаслідок пострілу з близької відстані навколо рани заглиблюються частки пороху, її краї обпалюються тощо.) В результаті маємо: "Тоді і тільки тоді, коли постріл зроблено з близької відстані, на тілі жертви залишається штанцмарка". Це судження еквіваленції або тотожності. Його структура виражається формулою: "А ↔ В". Вона читається так: "А еквіваленція В", "А еквівалентне В", "А тотожнє В". В усній мові і на письмі цей оператор звичайно передається граматичним сполучником "тоді і тільки тоді, коли..., то…"("якщо і тільки якщо..., то...", "коли і тільки коли ..., тоді...").
Тут ми маємо нову істиннісну залежність: "А ↔ В" істинне, якщо А і В одночасно істинні або одночасно хибні (тобто якщо ми ототожнюємо істинність з істинністю або хибність із хибністю). Якщо ж одне з них істинне, а друге хибне, то дане складне судження в цілому вважаться хибним (тобто не можна ототожнювати істинність із хибністю і навпаки). Точну характеристику функціонального значення оператора еквіваленції дає така таблиця:
|
А |
В |
А ↔ В |
|
1 |
1 |
1 |
|
1 |
0 |
0 |
|
0 |
1 |
0 |
|
0 |
0 |
1 |
Можна зауважити, що оператор еквіваленції є симетричним. Змінні А і В можуть входити до формули в довільному порядку, це не має значення з семантичної (істиннісної) точки зору. Вирази "А ↔ В" та "В ↔ А" рівносильні.
Логіка використовує ще один оператор – заперечення. Він позначається символом ¬ або рискою над відповідним виразом (це може бути і окрема змінна). Наприклад: A ¬А, ¬(А∨В). Читаються ці формули так: "не-А", "хибно, що має місце слабка диз'юнкція А і В". Семантична таблиця даного оператора виглядає так:
|
А |
A |
|
1 |
0 |
|
1 |
0 |
Розглянуті формули мають дуже важливе значення для того, щоб формалізувати інформацію. Цей процес, як ми вже казали (розглядаючи першу тему), полягає у виявленні логічної структури думки та фіксації її у вигляді формули. Він починається з виділення структурних елементів судження (висловлювання), що його треба формалізувати. Потім кожному з них треба дати позначення (для цього використовуються, як правило, великі букви латинської абетки: А, В, С тощо). Після цього встановлюються логічні зв'язки між структурними елементами і складається формула.
Інколи формалізувати інформацію буває досить складно. По-перше, вже названі граматичні сполучники – "і", "та", "чи", "або", "якщо..., то..." тощо – вживаються не завжди однозначно. Наприклад, "чи" не обов'язково повинне виражати слабку диз'юнкцію, а "якщо..., то..." – імплікацію. За змістом можуть бути сильна диз'юнкція та еквіваленція. По-друге, можуть вживатись також інші граматичні сполучники. Взагалі з'язки між думками можуть передаватися й іншими мовними засобами. Розглянемо приклади.
Який логічний зв'язок між судженнями "Цей злочин треба кваліфікувати як пограбування" і "Цей злочин треба кваліфікувати не як крадіжку" має місце у такому судженні: "Цей злочин треба кваліфікувати як пограбування, а не як крадіжку"? Позначимо перше просте судження через А, друге через В. Граматичний сполучник "а" звичайно виражає кон'юнкцію. Структура цього складного судження виражається формулою "А ∧ В".
Розглянемо тепер судження "Якщо С. майстер спорту із самбо, то Л.– фахівець з айкідо". Формально його можна вважати умовним через сполучник "якщо..., то...". Одначе між простими судженнями, які входять до його складу, нема причинного зв'язку. Те, що Л. фахівець з айкідо, зовсім не випливає з того, що С. – майстер спорту із самбо. Тому його можна розглядати і як судження кон'юнкції. Формула даного судження виглядає так само, як і в попередньому випадку (при цьому не має значення, яке з використаних простих суджень позначити через А, а яке – через В).
Існують також інші способи вираження кон'юнктивного зв'язку між думками. Саме такий зв'язок має місце, наприклад, у судженні "Підсудний заслуговує на покарання, але при його визначенні слід взяти до уваги обставини, які пом'якшують провину".
Якщо у нас є розділове судження, то треба вміти розрізняти слабку і сильну диз'юнкції. Граматичні сполучники "чи" і "або" можуть виражати як одну, так і другу. Наприклад, судження "Злочин було вчинено П. чи Д. " є невизначеним. Для того, щоб записати його формулу, треба знати, можуть бути підозрювані одночасно винними, чи злочин міг вчинити тільки один з них. Судження "Злочин було вчинено П. чи Д. (чи обома)" – це слабко-розділове судження, його формула: "А ∨ В" (яке саме з простих суджень буде позначене буквою А, а яке буквою В, не має значення). Розглянемо другий варіант: "Злочин було вчинено П. чи Д. (але тільки одним з них)". Це вже сильна (строга) ди"зюнкція. Логічна структура даного судження виглядає так: "А ∨ В" (зауваження щодо позначень залишається тим самим).
Проаналізуємо ще кілька розділових суджень: "Свідчення А. і С. не виключають одне одне, але не можуть бути одночасно хибними"; "Просте судження може бути стверджувальним або заперечним"; "Даний пальцевий відбиток належить тільки або господарю квартири, або його дружині"; "На нараді обов'язково буде присутнім хоча б один з експертів – М. чи К. ". У першому з них має місце слабка диз'юнкція, тому що тут можливі такі варіанти: істинними є обидва свідчення – і А., і С.; істинним є тільки свідчення А., в той час як свідчення С. хибне; істинним є свідчення одного лише С.. Аналогічну ситуацію маємо у останньому судженні. Не виключена можливість того, що на нараді будуть присутні обидва експерти – і М., і К., але виключена відсутність їх обох. Першому і четвертому судженням відповідає формула: "А ∨ В". Звернемось до другого судження. Просте судження не може бути одночасно стверджувальним і заперечним, хоча одну з цих двох характеристик воно має обов'язково. Тому це сильна диз'юнкція. Те ж саме можна сказати і про третє судження – один і той же пальцевий відбиток не може належати двом особам. Структура цих двох суджень виражається формулою: "А ∨ В".
Тепер візьмемо для прикладу судження: "Причетність до злочину Ш. необхідна і достатня для того, щоб визнати алібі М. "; "Свідчення Д.– достатня, але не необхідна підстава для того, щоб прийняти версію підозрюваного"; "Наявність у підозрюваного Л. можливості дістати вогнепальну зброю – необхідна, проте не достатня умова вчинення ним вбивства Д. "; "Алібі П.– єдина можлива умова алібі С.".
Проаналізуємо перше судження. Ми бачимо, що прості судження, які складають його, еквівалентні одне одному: з причетності до злочину Ш. випливає алібі М. і навпаки, алібі М. тягне за собою визнання винності Ш.. Формула цього судження виглядає так: "А ↔ В". У другому судженні еквіваленції нема – для прийняття версії підозрюваного можуть бути й інші достатні підстави, окрім свідчень Д.. Його формула має такий вигляд: "А → В", де буквою А позначено свідчення Д., а В – можливість прийняття версії підозрюваного. У третьому судженні також маємо імплікацію, проте якщо позначити наявність у підозрюваного Л. можливості дістати вогнепальну зброю через А, а вчинення ним вбивства Д.– через В, то формула набуває такого вигляду: "В → А", тобто підставою (засновком, антецедентом) є В, а наслідком (висновком, консеквентом) – А. Справді, якщо вбивство Д. скоєно Л., то це означає, що в останнього була можливість дістати вогнепальну зброю. А наявність у Л. такої можливості ще не означає, що Д. забив саме він. Останнє з наших суджень, очевидячки, слід віднести до еквіваленції. Адже з алібі П. випливає алібі С., а з алібі С.– алібі П.. В даному випадку, як і в першому, структура складного судження виражається формулою "А ↔ В".
Ми бачимо, що еквіваленція за своїм логічним змістом протилежна сильній диз'юнкції, точніше, рівносильна її запереченню. Можна записати формулу: (А ↔ В) ≡¬ (А ∨ В). Зауважимо також, що еквіваленція відноситься до імплікації аналогічно до того, як сильна диз'юнкція відноситься до слабкої. Суть цієї аналогії полягає ось у чому: формула "А ∨ В" означає, що В є однією з можливих альтернатив по відношенню до А (поряд з перетином, або одночасною істинністю А і В); в той же час формула "А ∨ В" містить твердження про те, що В необхідно розглядати як єдину можливу альтернативу А (і навпаки) у межах дії підстави їх виділення. Подібно до цього формула "А → В" означає, що А є однією з можливих підстав істинності В, тоді як з формули "А ↔ В" випливає, що А являє собою єдину можливу підставу для істинності В (й навпаки).
Формули складних суджень потрібні для розуміння мови логіки висловлювань, тобто штучної мови, призначеної для аналізу логічної структури складних висловлювань.
Для аналізу наступної теми, яка стосується законів логіки, нам потрібно мати уявлення про так звану тотожно-істинну формулу. Це формула, яка залишається істинною при всіх семантичних значеннях змінних, що входять до її складу.
Можна взяти, наприклад, формулу (А → В) ↔ (¬А ∨ В). Щоб визначити, чи є вона тотожно-істинною, треба побудувати її семантичну таблицю. При цьому ми звернемось до семантичних таблиць імплікації, еквіваленції, заперечення і слабкої диз'юнкції:
|
(А → B) |
↔ |
¬А ∨ B) |
||||
|
1 |
1 |
1 |
1 |
0 |
1 |
1 |
|
1 |
0 |
0 |
1 |
0 |
0 |
0 |
|
0 |
1 |
1 |
1 |
1 |
1 |
1 |
|
0 |
1 |
0 |
1 |
1 |
1 |
0 |
Дана формула є тотожно-істинною, оскільки стовпчик семантичних значень всієї формули (він розташований під символом еквіаленції) містить тільки значення "істинне".
Якщо у підсумковому стовпчику значень формули є тільки "хибне", то така формула називається тотожно-хибною. Для повноти картини слід сказати, що існують також формули, які при деяких значеннях змінних мають загальне значення "істинне", при інших – "хибне". Такі формули називають виконуваними. Приклади таблиць останніх двох типів виглядають таким чином:
|
¬А ∨ B) |
↔ |
(A ∧ ¬В |
||||
|
0 |
1 |
1 |
0 |
1 |
0 |
0 |
|
0 |
0 |
0 |
0 |
1 |
1 |
1 |
|
1 |
1 |
1 |
0 |
0 |
0 |
0 |
|
1 |
1 |
0 |
0 |
0 |
0 |
1 |
|
((A ∨ B) ∧ B) ↔ A |
||||||
|
1 |
0 |
1 |
0 |
1 |
0 |
1 |
|
1 |
1 |
0 |
0 |
0 |
0 |
1 |
|
0 |
1 |
1 |
1 |
1 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
1 |
0 |
Якщо формула містить не дві, а, скажімо, три змінних, то семантична таблиця містить вдвічі більше рядків – вісім, якщо змінних чотири – шістнадцять тощо.
3. Логічні властивості правових норм
Розглянемо логічні властивості правових норм, передусім їх структуру.
Почнемо з того, що нормативна логіка в загальному вигляді — це розділ сучасної формальної логіки, що вивчає властивості і способи їх вживання і вираження в формулах.
У нормативній логіці вивчається один з видів приписувального міркування, яке пов'язане з виконанням людиною певних дій і виявляється в таких формах, як ухвалення рішень, пред'явлення вимог, віддавання команд і т.д. Ці форми мають такі специфічні властивості, які змушують створювати для їх аналізу специфічну логічну теорію або модифікувати наявні логічні теорії.
Нормативна логіка займається освітою і з'єднанням нормативних висловлювань або, інакше кажучи, займається логічною структурою прескриптивної мови, яка виражає поведінку по здійсненню тієї чи іншої норми. Мета всіх формально-логічних перетворень у сфері розпоряджень, імперативів — аргументувати норми і вимоги, обгрунтувати їх як безперечні і очевидні.
Розглянемо специфіку правових норм. Почнемо з поняття правової норми.
Для юриспруденції правильне рішення питання про природу і логічну структуру норм права є однією з найважливіших умов, що забезпечують одноманітність і точне застосування та виконання юридичних законів правозастосувальними органами, установами, організаціями і громадянами.
Під нормами в сучасній логіці розуміють усі пропозиції (висловлювання), які виражають, що щось повинне бути здійснене незалежно від того, чи виражено це категоричним чином або як пропозиція, рекомендація, побажання, заклик і т.д. Нормами в широкому сенсі є і прагматичні правила, правила спортивних ігор, інструкції по вживанню продуктів, інші рекомендації.
Зіставлення різних фрагментів природної мови дозволяє виділити ряд схожих моментів вживання терміну "норма" в контексті, близькому або співпадаючому з уявленням про правову норму (на відміну від інших за формою нормативних актів). По-перше, граматичною формою нормативного висловлювання, як правило, виступає імперативна пропозиція (висловлювання), що є прескрипцією, тобто вимога, приписуюча виконання або утримання від виконання певної дії.
По-друге, до норм в правовому контексті відносять такі розпорядження, які носять регулятивний загальний характер.
По-третє, нормативними в правовому сенсі є розпорядження, порушення яких завжди призводить до певних несприятливих наслідків, до того, що називається утратою, збитком, погіршенням стану справ і що узагальнюється поняттям "санкція".
Відзначені три ознаки служать достатньо чітким критерієм для того, щоб відрізняти правові норми від інших примушувально-регулятивних розпоряджень типу команд, наказів, рішень.
Тут і далі під нормою права ми розумітимемо наказане офіційним органом і спрямоване на охорону панівних соціальних інтересів загальнообов'язкове правило поведінки, регулююче взаємини між людьми, організаціями і органами влади, невиконання якого тягне за собою застосування передбачених нормами юридичних санкцій.
Норма права виступає регулятором особливого роду суспільних відносин, що іменуються правовідносинами. У правовідносинах "праву" завжди кореспондує "обов'язок": всяке право передбачає обов'язок, і навпаки.
Правовідношення, будучи фундаментальною юридичною категорією, характеризується певними логічними властивостями. По-перше, правовідношення між суб'єктами — це завжди двомісне відношення. Символічно його можна виразити як х R уабо R(x,y). Це означає, що попередньому члену правовідношення (х) надається право пред'явити певні вимоги, а на подальший член правовідношення (у) накладається обов'язок задовольнити пред'явлені вимоги.
Правовідношення нерефлексивне, тобто ¬R(x,x),бо безглуздо пред'являти до самого себе правову вимогу і приймати обов'язки до його виконання. Корелятивність "права" і "обов'язку" служить показником стійкої асиметричності правовідносин.
Правовідношення відноситься до нетранзитивних відношень. У будь-якому випадку, якщо х знаходиться відносно Rдо у, а цей останній в такому ж відношенні до р, то невірно, що х буде відносно Rдо р.
Тепер звернемось до логічних властивостей правових норм. Почнемо з логічного значення істинності правових норм. Якщо ми звернулися до логічнх властивостей правових норм, які повинні так чи інакше виразити в логічному аспекті, нас повинні зацікавити перш за все такі відношення, як проходження, сумісність і несумісність правової норми. Що означають ці відношення, найчіткіше пояснюється за допомогою поняття істини і різних функціональних понять. Наприклад, про логічне проходження одного з іншого кажуть, що якщо останнє істинне, то перше теж повинне бути істинним.
Проте існує думка, згідно якій норми не мають істиннісного значення, не є ані істинними, ані хибними. Тоді, щонайменше, сумнівно, що одна норма логічно виходить з іншої. Можливо, підстави проходження — зовсім не формально-логічного порядку. Для того, щоб відповісти на це питання, слід заздалегідь зробити ряд істотних уточнень.
Першим з них буде поділ деонтичних формул на нормативні пропозиції і висловлювання про норми. Їх змішення може привести до деяких логічних помилок. Висловлювання про норми стверджують або заперечують, що що-небудь є обов'язковим, дозволеним або забороненим. Вони вказують, що існує або не існує така-то і така-то норма. Ці висловлювання є або хибними, або істинними і підкоряються законам звичайної логіки.
Нормативні пропозиції мають приписувальний сенс, за допомогою їх що-небудь зобов'язується, забороняється або дозволяється. Вони не виражають істинні чи хибні висловлювання. Принаймні, в такій інтерпретації деонтичні формули не утворюють клас виразів, в яких значення істинності має найбільший інтерес.
З певними підставами можна твердити, що правові норми відображають певні суспільні відносини або адекватно, або неадекватно, і з цієї точки зору вони мають статус істинних або неістинних.
Такий підхід — ключ для знаходження оцінки, що виконує в нормативних висновках роль, аналогічну ролі істинності висловлювань. Цю оцінку можна назвати нормативною істиною, а відповідну норму — нормативно-істинною. Норма, не відповідна запитам вимогам суспільного розвитку, є нормативно-хибною, а оцінка її — нормативною хибою. Перевіряється істинність таких норм на практиці.
Тим самим питання про істинність правових норм вимагає чіткого розрізнення принаймні істинності гносеологічної та нормативної.
Нормативні оператори "обов'язково", "заборонено" не можуть бути самостійними вираженнями істинності або хибності хоч би тому, що не можна стверджувати істинність або хибність виразу "заборонено", якщо невідомо, що заборонено. Питання про істинність і хибність нормативної пропозиції може виникнути лише тоді, коли до нормативного предиката приєднаний аргумент, тобто якщо йдеться про пропозицію "повинне бути р" (Мр).
Мр можна вважати істинним лише тоді, коли ми розуміємо його як висловлювання про те, що відоме р повинне бути. Навпаки, щодо норм питання про істинність або хибність, принаймні, в гносеологічній інтерпретації, не має сенсу. Візьмемо за приклад нормативну пропозицію "Боржник зобов'язаний виконати борг належним чином в строк". Дана пропозиція не говорить про те, що за ним стоїть певна дійсність, а тільки вказує, яким чином боржник повинен чинити, приєднує до поведінки боржника оператор "обов'язково". Якщо в наведеній пропозиції ми маємо на увазі твердження, що боржник зобов'язаний належним чином поводитися відповідно до певного закону, або що така норма міститься в законі, то це істинно або помилково, але зовсім не в нормативному сенсі.
Отже, визнання і гносеологічної і нормативної істини стосовно нормативних пропозицій не в змозі нам допомогти в розкритті системних властивостей правових норм, визначити відношення їх проходження і сумісності.
Тут необхідно зробити ще одне уточнення. Воно полягає у виділенні логічного контексту істини як відносно самостійного. Перший стосується значення істинності висловлювання самого по собі. Другий стосується значення істинності формального зв'язку між висловлюваннями. У дескриптивній логіці осмисленим є вживання обох значень істини. Істинним (або хибним) може бути як висловлювання "Всі студенти юридичного інституту — чоловіки", так і логічний зв'язок між висловлюваннями типу "Йде іспит" і "В залі засідань суду ясно". Причому, істинність самого дескриптивного висловлювання визначає і істиннісне значення його логічного зв'язку з іншими висловлюваннями.
У нормативній логіці, як було показано, перше значення поняття істини неприйнятне. Безглуздо, наприклад, приписувати нормативному висловлюванню "Заборонено здійснювати крадіжки" значення істинності або хибності. У нормі лише фіксується саме її існування.
Але чи можна вживати поняття істини в другому значенні? Чи діють в системі норм хоч би прості формально-логічні відношення, однакові з дескриптивною логікою? Таке вживання було осмисленим, бо нетривіально пояснює відношення проходження і сумісності норм права.
Система правових норм будується, обов'язково виходячи з вимоги несуперечності, внутрішньої узгодженості всіх нормативних пропозицій (висловлювань). Означає, якщо ми виходимо з визнання застосовності правил дескриптивної логіки до норм, то, наприклад, взаємовідношення суперечливих нормативних пропозицій повинне підкорятися формально-логічним законам, зокрема, закону виключеного третього. Тут — вузловий момент всіх міркувань про можливість формально-логічної інтерпретації нормативних систем.
Суперечливі правові норми мають свої особливості.
Розглянемо три варіанти виразу несумісності суперечливих нормативних пропозицій.
- Істинність і помилковість нормативного висловлювання можна представити як взаємозаперечливі значення цих висловлювань в системі норм. Так, якщо як істинність норм буде прийняте її ствердне вживання, то, відповідно, хибним буде її негативне вживання. Наприклад, вирази Мр і ¬(Мр), тобто "стверджується, що повинне бути p" і "заперечується, що повинне бути р" несумісні. Причому, третьої можливості немає. Отже, в цьому випадку закон виключеного третього діє, і взаємозв'язок двох суперечливих нормативних висловлювань може бути коректно інтерпретована через двозначну логіку в сенсі протилежності "істинність — хибність". Таке твердження цілком відповідає природному мисленню.
- Візьмемо висловлювання Мр і ¬Мр, а саме "повинне бути р" і "не повинне бути р". Тут також видно, що третьої можливості немає. Закон діє. Обидва висловлювання є такими, що стверджують. У першому випадку стверджується "належність р" і в другому випадку стверджується "неналежність р". Суперечність їх підтримується за рахунок того, що вони вживаються, по суті, не як нормативні пропозиції (висловлювання), а як такі, що стверджують висловлювання.
- Порівняємо пару тверджень: Мр і М¬р, тобто "повинне бути р" і "повинне бути не-р". Тут третя можливість не виключена. Можна стверджувати, що не повинне бути ні р, ні не-р. Уявимо собі пропозиції "Громадяни повинні в час У виходити з будинку" і "Громадяни повинні в час В не виходити з будинку". Але з цих пропозицій не повинно виходити жодне, ні інше, оскільки громадяни, за нашим правилом, можуть вільно в час У виходити з будинку або залишатися в ньому. Вказані норми Мр і М¬р, поза сумнівом, суперечливі, але в їх взаємовідношенні, як видно, закон виключеного третього не діє.
Проте, дуже важливо відзначити, що хоча за формою висловлювання Мр і М¬р, поза сумнівом, суперечливі, їх крім цього можна зрозуміти і як самостійні неузгоджені в деякій нормативній системі норм, одна з яких не просто заперечує іншу. Саме тому норми Мр і М¬р не виключають іншу можливість. Даний факт вказує на специфічну для нормативної логіки проблему, яка в області права набуває практичного значення. Це проблема розуміння суперечності або несуперечності нормативних систем і в цілому права.
Отже, по-перше, у двох варіантах йдеться про звичайну дескриптивну логіку, в якій пропозиційними змінними виступають висловлювання про норми. Внутрішня їх структура абсолютно не впливає на характер логічних зв'язків. У третьому варіанті ми маємо справу з власне нормативною логікою, в якій замість закону виключеного третього діє правило несумісності суперечливих нормативних пропозицій. Дане правило має в праві величезне значення; його порушення тягне за собою послаблення законності та юридичних гарантій для громадян. Воно не носить, проте, характеру логічного закону, аналогічного законам загальної формальної логіки, але є категоричною правовою вимогою, постійне виконання якої є невід'ємною частиною та передумовою забезпечення бажаного рівня правопорядку.
Зі сказаного зробимо висновок, що немає раціональних підстав заперечувати застосовність правил і законів логіки висловлювань в їх дійсному значенні до нормативних пропозицій.
ЛІТЕРАТУРА
Основна
- Вандишев В.М. Логіка. Основні поняття і принципи: навчальний посібник. К: Кондор - Видавництво, 2016. 300 с.
- Жеребкін В.Є. Логіка: Підручник. К.: Знання, 2011. 262 с. Шифр Ю4 Ж592.
- Карамишева Н.В. Логіка (Теоретична і прикладна): навчальний посібник. К: Знання, 2011. 455 с.
- Конверський А.Є. Традиційна логіка. Підручник для студентів навчальних закладів вищої освіти усіх спеціальностей. - К.: Центр учбової літератури, 2019. 452 с.
- Конверський А. Є. Логіка: підручн. для студ. юрид. фак-тів ВНЗ. К.: ЦУЛ, 2012. 335 с. Шифр Ю4 К64.
- Логіка для правознавців : навч. посіб. / [О. О. Бандура, О. І. Гвоздік, В. М. Кравець, Р.В. Михайленко та ін.]. К.: Національна академія внутрішніх справ, 2016. 144 с.
- Логіка: Навчальний посібник / С. В. Сторожук, І. М. Гоян, І. С. Матвієнко. К.: Вадекс, 2020. 370 с.
- Мозгова Н.Г. Логіка: навчальний посібник. К.: Каравела, 2011. 247с. Шифр Ю4 М747.
- Павлов В.І. Логіка у запитаннях, відповідях і аргументаціях. К.: Центр учбової літератури, 2008. 408 с.
- Хоменко І.В. Логіка: теорія і практика. К.: Центр учбової літератури, 2022. 378 с.
- Щербина О. Ю. Логіка для юристів : курс лекцій / О. Ю. Щербина. – вид. 2-ге, допов. і перероб. К. : Юридична думка, 2009. 264 с.
- Гвоздік О. Формальні та неформальні аспекти логіки розслідування. Філософські та методологічні проблеми права. 2021. №2 (22). С. 56-63.
- Гнатюк Я.С. Некласична логіка: Курс лекцій із практикумом. Івано-Франківськ: Симфонія форте, 2014. 191с. Шифр Ю4 Г560.